Compilers Pt. 1 -- Scanner

Scanners

The goal of a compiler is to take our source file (the file that the programmer writes and wants to run), and translate it into machine code that can be run directly on some target hardware (usually the programmer's own computer). When undertaking large tasks, it's a smart idea to break the problem down into manageable subtasks. The first subtask that compilers take is performing lexical analysis on (or scanning) said file.

Compilers do that by reading the source file and breaking the lines down into a list of words and punctuation. The compiler can then loop through each word in our source file and create a token -- a tuple (pair) consisting of the word in question (i.e. lexeme), and it's part of speech, (i.e. syntactic category). Compilers do this for two reasions -- first, to determine if the program is even valid, and secondly to annotate the syntactical structure of the program, so that we have clues on how to process it in the subsequent steps. The scanner is the only part of the compiler that touches every character of the source file, therefore it's wise to optimize for speed here.

Scanners read the source file character by character, grouping them into words, and then dropping the words into buckets depending on their category. Scanners identify the words in a stream of characters by using recognizers. Recognizers encode a more formal representation of the set of possible structures of valid words in our source program called deterministic finite automata (DFA). A finite automaton is a five-tuple consisting of:

• The finite set of states in the recognizer
• The recognizer's alphabet (set of possible characters)
• The recognizer's transition function -- the function that determines how we move from state to state
• The initial state
• The set of states that we can validly end a word with (accepting states)

Recognizers repeatedly apply our transition function to the pair (current state, next input character) to determine our subsequent state. There are two possible cases that indicate errors -- if our finite automaton reaches a designated error state, or if a word ends, and our finite automaton is in a nonaccepting state. Finite automata can be visualized with cyclic transition diagrams:

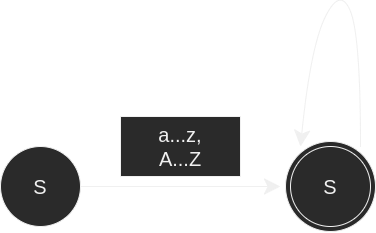
Each circle represents a possible state, double circles represent accepting states, and arrows represent the corresponding transition functions for a given state. The set of words accepted by a finite automaton represents a language, and these diagrams describe how to spell every valid word within the language.

These diagrams give us humans a good mental image for the flow of our recognizer. However, computers cannot (easily) understand such diagrams. So we need another abstraction to represent our finite automata in a more computer-friendly fashion.

Regular Expressions are a concise and powerful notation for specifying search patterns in text. In compilers, they are used to specify the microsyntax of our source language. A set of strings that can be represented by a regular expression is called a regular language.

Complex regular expression can be built up from three basic operations: alternation (union in set-theoretic terms) of two regular expressions joined with the | symbol, concatenation of two regular expressions, and closure denoted by an asterisk which represents a repetition of zero or more words from a regular expression. For example, a regular expression representing our previous finite automaton for Algol-style identifiers would be ([a...z] | [A...Z])([A...Z] | [a...z] | [0...9]). The order of precedence goes as follows: parentheses, closure, concatenation, alternation.

Since regular expressions can be composed in a nested fashion to describe more complex regular expressions, we can construct a regular expression for our entire source language by alternating regular expressions for each syntactic category in said source language. Regular expressions can get hairy quickly. For example, here's the SOTA regex for validating email addresses. Luckily, the cost of operating a finite automaton scales in proportion to the length of the input, rather than the complexity of the regular expression or the number of states in the finite automaton.

For the compiler I will be writing, our source language is a subset of C, called C0. More information on the C0 specification can be found here. Keywords include: int, bool, string, char, void, struct, typedef, if, else, while, for, continue, break, return, assert, error, true, false, NULL, alloc, alloc_array. Click here to see an exhaustive list of transition diagrams for C0's finite automata.

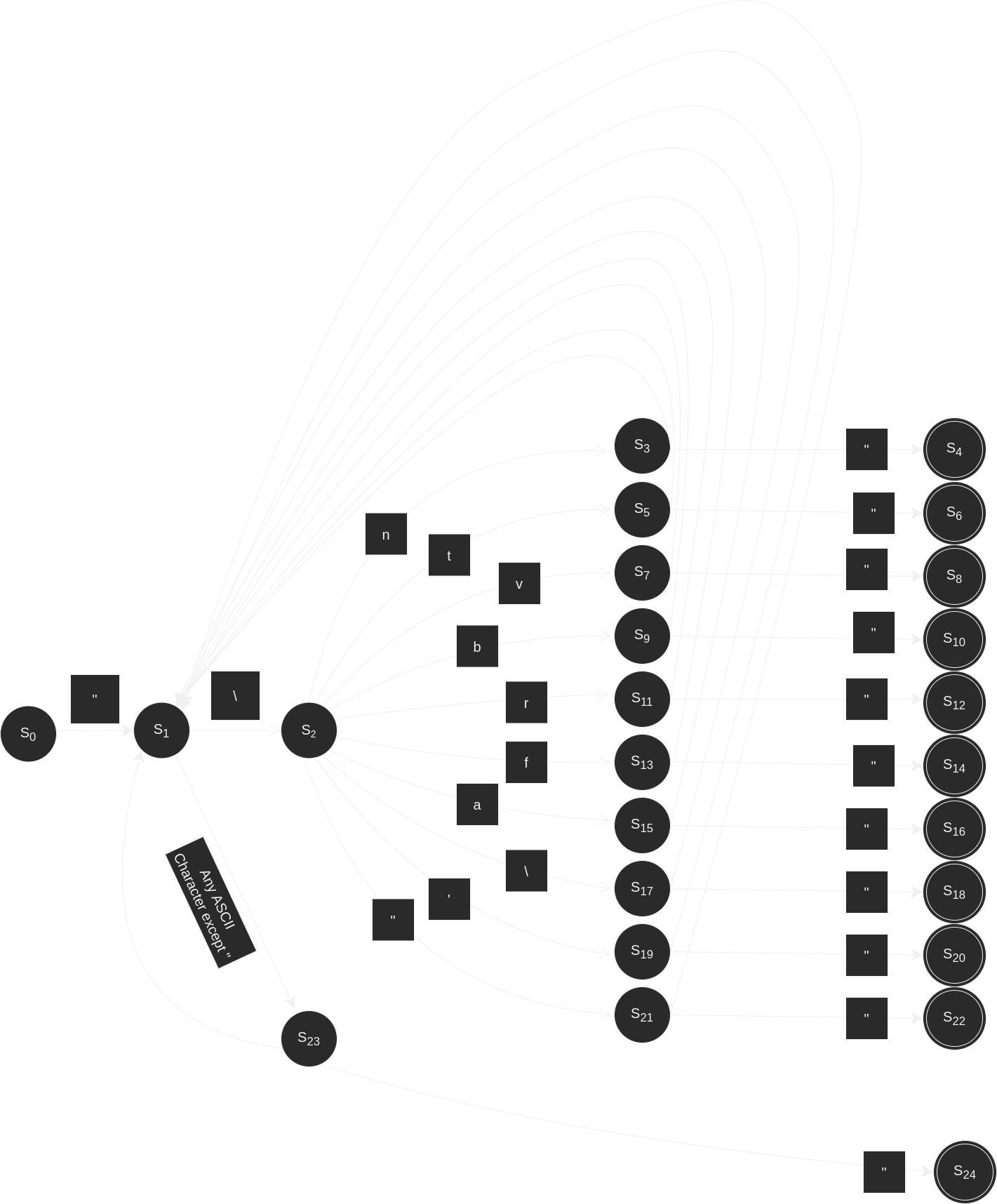
For the sake of brevity, we'll handwaive over the more formal language theory. When creating a scanner, you typically define the microsyntax for each syntactic category using regular expressions, then combine them into one large regular expression. Subsequently you'd want to generate a nondeterministic finite automaton (NFA) from the regular expression using Thompson's construction. After you have your NFA, you convert it into a DFA via the Subset/Powerset construction. Once we have our DFA, we can optimize it's performance by minimizing it's size. By minimizing our DFA, we allow it to better fit into the lowest possible level of cache memory thus improving memory access times. For now, though, let's skip the formalism and just use my handcrafted, non-minimized DFA to get to our MVP faster. I may come back later to optimize. Once we have our DFA, we have a few options for implementing the scanner: table-driven scanners, direct-coded scanners, and hand-coded scanners.

Both table-driven and direct-coded Scanners basically use procedural macros called scanner generators that take regex's as input and simulate their corresponding DFAs, typically in O(1) time per character (the complexity constant tends to be slightly higher in table-driven scanners due to an extra table lookup). On the otherhand, many compilers use hand-coded scanners. That's the route we'll take as well.

Hand-Coded Scanners

While direct-coded scanners tend to simplify the simulation of our DFA, hand-coded scanners allow the compiler writers to better fine tune the scanner's performance along specific paths, and customize it's output to more ergonimically be passed to the parser. When implementing a hand-coded scanner, there are two areas to look out for optimization: in the handling of the input stream, and in the transition table. However, since this isn't a production compiler, let's just get out an MVP first.

In our hand-coded scanner, we will use do things the Rusty way using iterator adapters and taking adavantage of std::str's char_indices. After reading our source file into a string, we then pass it to the scan() function which returns a vector of tokens. Once we have our source string, we will call the char_indices() and peekable() string methods on it. Char_indices() gives us an iterator in which each element is a tuple containing a character and it's corresponding index. We will use this index to give localized syntax error reports to the source authors. Additionally, peekable() gives us the opportunity to 'peek' at the next character (view w/o consuming) which really comes in handy. With this pattern, we can loop calls to next(), while they return Some((index, character)), hence looping for as long as there are characters in the string.

We can then match against the second inner element of Some((index, character)) to get the next character. Once we have the next character we can either return the appropriate token, if that represents a single character accepting state in our DFA's (e.g. Seperators: '{', '}', ';', ',', etc.) If, however, there is more than one possible accepting state along the current path, we need a way to determine which branch we should continue down. For example, in the case we encounter the '<' symbol, there are a few possible accepting branches. The first is simply the binary operator "less than" '<'. The second is the binary operator "shift left" '<<' for bit manipulation. The third is the binary operator "less than or equal" '<='. And the last is the assignment operator "shift left assign" '<<='. This is where the peek() method comes in clutch. We can peek at the next character and conditionally consume it if it matches a possible alternate accepting branch.

For most DFA paths, it's simply rinse a repeat -- mapping the appropriate control flow to each permutation. However, there are a few quirks.

Identifiers are begun with an alphabetic character and continue until a non-alphanumeric (including underscores) character is encountered. Decimal Numbers are begun with numeric characters and continue until a non-numeric character is found. Strings are essentially anything wrapped in a pair of double quotes. Some characters are particularly sensitive in Rust. When we try to match for them, we can't write them as we normally do because the Rust syntax rules interpret them as syntax instead of as their UTF-8 values as we intend. These include double quote, single quote, and backslash. To tell the Rust compiler we just want the UTF-8, we have to escape these characters (by prepending them with a backslash). Additionally, there are tokens whose characters are the exact same, but depend on their context. For example, the asterisk symbol ( * ), it can represent the binary multiplication operator, or the unary pointer operator. We can check the previous token by calling the last() associated method on our vector of tokens collected so far.

To get an idea of the structure of the scanner check out this code sample:

fn scan(source: String) -> Vec<Token> {
    ...
    let mut char_indices = source.char_indices().peekable();
    while let Some((index, character) = char_indices.next()) {
        let token = match character {
            // current token = '-', peek at the next character 
            '-' => match char_indices.peek() {
                // "-="
                Some((_, '=')) => {
                    // check for possible alternate accepting states, 
                    // consume the next character if it matches 
                    char_indices.next();
                    // Return appropriate accepting state
                    Token::AsnOp(AsnOp::DecAsn)
                },
                // "--"
                Some((_, '-')) => {
                    char_indices.next();
                    Token::PostOp(PostOp::Dec)
                },
                // "->"
                Some((_, '>')) => {
                    char_indices.next();
                    Token::BinOp(BinOp::FieldDeref)
                },
                // other
                _ => match tokens.last() {
                    // "<identifier or number>-"
                    Some(Token::Num(_) | Some(Token::Id(_))) => Token::BinOp(BinOp::Minus),
                    // "!<identifier or number> - <identifier or number>"
                    _ => Token::UnOp(UnOp::UnaryMinus),
                },
            },
            ...

For identifiers, we will essentially loop the previously seen conditional iteration on our char_indices iterator with a pattern that is similar to the take_while() iterator adapter with one key difference. When using take_while(), the predicate that we check against is evaluated using next(). This means the next element is consumed each time we want to check the next character -- creating a problem for us; we only want to consume the next character, if it is a valid extension of our current state. If it is not, we want to either begin consuming the next token, or report an error back to the end user.

If we were to use take_while(), when the token stops matching it's acceptable pattern, the character immediately following the token is thrown away. Usually this next character is a space so we don't notice the problem right away. However, if we were to, say initialize a pointer to an integer, we would write "int*". But using take_while(), the identifier pattern reads the keyword "int", then after checking the 't', it would call next(), encounter the '*' and throw it away because it does not belong to the set of acceptable characters for an identifier instead of tokenizing it.

We have to do the same pattern for numbers. Consider the case where we want to perform arithmetic -- the space between number and operator is optional (12*2 == 12 * 2). Take_while() would leave us with "12" and "2", sabotaging our semantics. We can fix this problem by implementing a conditional version of take_while():

...
// In the wildcard case (still matching against the next character), 
// we check if the character is alphabetic (in the case of identifiers), 
// or if the character is numeric (then differentiate between decimal and hexadecimal)
_ => {
    let mut s = character.clone().to_string();
    let mut stop_flag = false;
    if character.is_alphabetic() {
        while !stop_flag {
            // check before consuming
            if let Some((_index, next_char)) = char_indices.peek() {
                if (next_char.is_alphanumeric || *next_char == '_') && *next_char != ' ' {
                    // condition is true, so we are good 
                    // to consume next element
                    if let Some((_index, next_char)) = char_indices.next() {
                        // concatenate character to string 
                        s.push(next_char);
                    }
                } else {
                    // condition is false, don't consume next element 
                    // and stop looping
                    stop_flag = true;
                } 
            } else {
                // No subsequent character (peek returned None) so 
                // stop looping
                stop_flag = true;
            }
        }
        // then match against keywords -- return keyword token
        // if a match is found
        match s.as_str() {
            "int" => Token::Keyword(Keyword::Int),
             ...
             _ => Token::Id(Id::Id(s)),
        }
    } else if character.is_numeric() {
        let mut hex_flag = false;
        while !stop_flag {
            if let Some((_index, next_digit)) = char_indices.peek() {
                // decimal -- base-10
                if next_digit.is_digit(10) {
                    ...
                // hexadecimal -- base-16
                } else if next_digit.is_digit(16) {
                    ... 
                }
            }
        }
    } else {
        panic!("Unrecognizable character: {}", character),
    }
}
...

And that's the gist of our handcoded scanner! Not too bad right? Of course, we trimmed the scanner to avoid an intimidating wall of code, if you'd like to see the scanner in full, check out this section of the git repo, and if you'd like to check out how we broke down the token syntactic categories, look here.

From there, what's next is to pass our vector of tokens onto the parser, so that we can begin to make sense of them. Click here to follow along to the next post!